Devoir Surveillé 6

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

télécharger le document au format open office

Exercice 1 (6 points)

Une urne contient 5 boules indiscernables au toucher : 1 boule verte valant 1 point , 2 boules bleues valant chacune 2 points et 2 boules rouges valant chacune 3 points.

1. On tire au hasard une boule dans l'urne.
   Calculer la probabilité des évènements suivants : A: « obtenir une boule bleue » ; B : « obtenir exactement un point » et C : « obtenir au moins 2 points ».

2. On tire successivement et sans remise 2 boules dans l'urne.
   a) Déterminer le nombre de tirages différents possibles à l'aide d'un arbre.
   b) Calculer la probabilité des évènements suivants :
   D : « obtenir deux boules de la même couleur »
   E : « obtenir exactement 4 points ».

Exercice 2 (4 points)

Un dé pipé dont les faces sont numérotées de 1 à 6 est tel que :

p(1) = p(2) = p(3) = p(4) = p(5) = 0,1.

1) Calculer p(6).

2) Calculer la probabilité des événements suivants :

A: “ le numéro est pair “;

B : “ le numéro est strictement supérieur à 4 “;

C : “ A U B “.

Exercice 3 (6 points)

Sur la figure ci-contre, C_f est la courbe représentative d'une fonction f dérivable sur IR.

d₄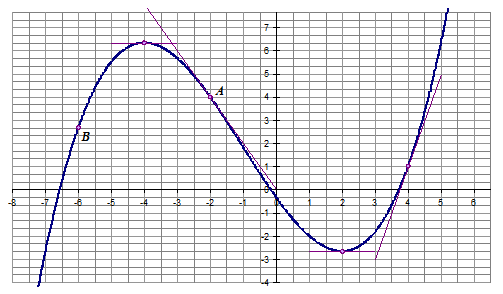

1. Déterminer graphiquement , et .

2. Déterminer graphiquement les nombres dérivés et .

3. La tangente à la courbe C_f au point A d'abscisse − 2 passe par l'origine du repère. Déterminer .

4. La tangente T à la courbe Cf au point est parallèle à la droite d4. Déterminer puis, donner une équation de la tangente T à la courbe au point B. Tracer cette droite sur le graphique précédent.

Exercice 4 (5+2 points)

Dans chaque cas, f est une fonction définie et dérivable sur un intervalle I. Calculer .

1. f est définie sur par

2. f est définie sur par

3. f est définie sur IR par