Devoir surveillé
Devoir surveillé
La rédaction prendra une part importante dans la notation.
Exercice 1 :
(un)et
(
)
sont les suites définies pour tout entier naturel n par :
.
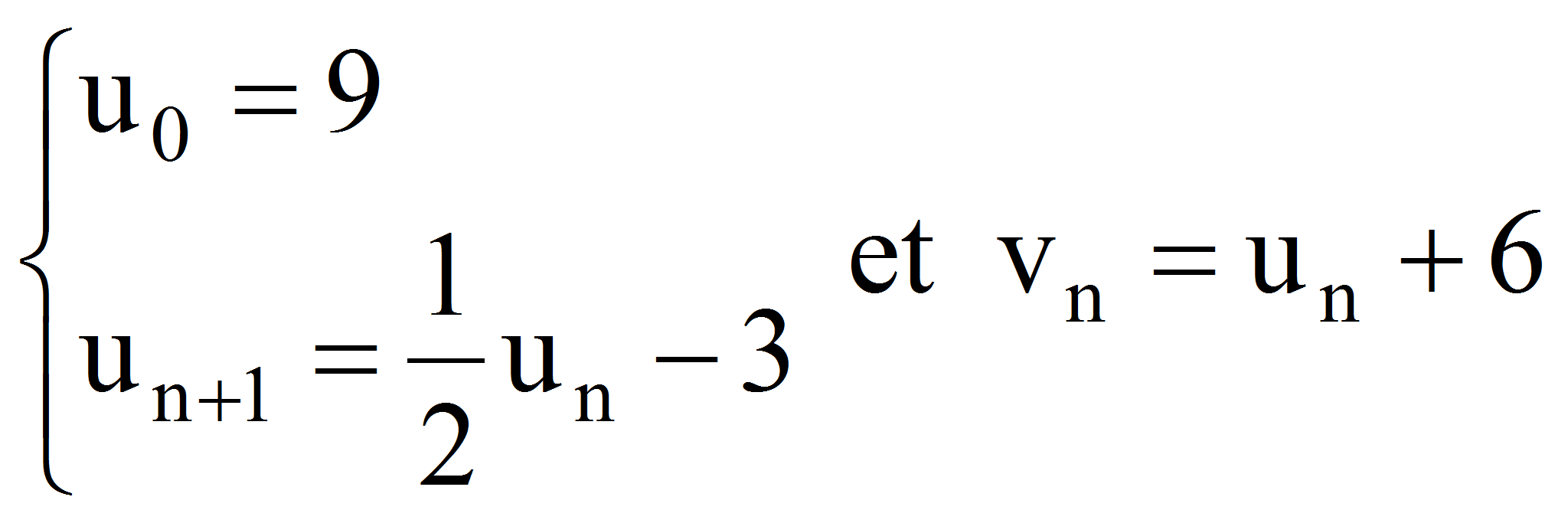Montrer
que la suite ()
est géométrique à termes positifs.
En déduire l’expression
de 
en fonction de n.
Calculer les sommes :
Exercice 2 :
On désigne par f
la fonction définie sur ]-1;
[
par : 
, et par C sa courbe représentative dans un repère orthonormal
(O, 
,
).
Etudier les variations de f .
Etudier les limites de f. En déduire son tableau de variations.
Déterminer l’équation de la tangente T à C en 1.
Démontrer que la droite d'équation
est asymptote à C en 
.
Déterminer la position relative
de (C) et de la droite Δ d’équation 
.
En
quel(s) point(s) de la courbe (C) observe t’on une tangente de coefficient
directeur 
?
Pour
contacter le webmaster 
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.
