Devoir surveillé 3
Devoir surveillé 3
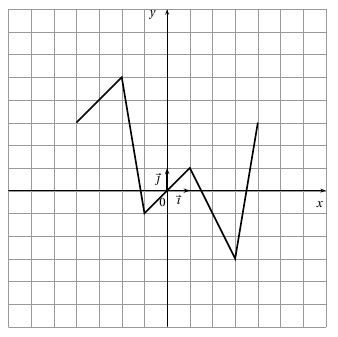
Exercice 1 (4 points)
Soit f la fonction définie sur l'intervalle [-4;4] dont la courbe
représentative ![]() dans un repère orthonormé
dans un repère orthonormé ![]() est donnée ci-dessous.
est donnée ci-dessous.
Tracer les courbes représentatives des fonctions ![]() et
et ![]() .
.
Exercice 2 (4 points)
Soit u une fonction définie sur ![]() dont le tableau des variations est le suivant :
dont le tableau des variations est le suivant :

Dresser le tableau des variations des fonctions l et m définies
pas : ![]() et
et ![]() .
.
 Exercice
3 (6 points)
Exercice
3 (6 points)
La courbe ci-contre est la représentation graphique d'une fonction f
définie sur ![]() .
.
A partir du graphique, répondre aux questions suivantes :
1) Quelles sont les solutions de l'équation ![]() ?
?
2) On considère la fonction g définie pour tout réel
x par ![]() .
.
a) Exprimer g comme la composée de deux fonctions dont l'une
est f.
b) Calculer ![]() .
.
c) Établir le tableau des variations de la fonction g. Préciser
l'extremum de la fonction g.
Exercice 4 (6 points)
1000 élèves de plusieurs lycées différents ont mesuré la densité du laiton par la méthode du flacon. Les résultats , arrondis au dixième, ont été regroupées dans le tableau suivant :
Calculer la moyenne de cette série statistique, en donner un  arrondi
au dixième.
arrondi
au dixième.
On augmente de 7% chacune des valeurs de la série.
Calculer la nouvelle moyenne.
Quel est le pourcentage de résultats qui se trouvent dans l'intervalle
![]() ?
?
Calculer la médiane, les premier et troisième quartiles.