Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

DEVOIR SURVEILLE N°3
Cliquez ici pour obtenir le document au format Word97 compressé avec winzip.

Exercice n°1 : 6 points

On désigne par i le nombre complexe de module 1 et d'argument .

On pose : .

1)      a) Mettre  sous forme algébrique.
b) Mettre Z sous forme algébrique.

2)      a) Déterminer le module et un argument du nombre complexe , puis le module et un argument du nombre complexe .
b) Déterminer le module et un argument du nombre complexe .
c) Déduire des questions précédentes une écriture trigonométrique de Z.

3)      En comparant les écritures algébriques et trigonométrique de Z, déterminer les valeurs exactes de .

Exercice n°2 : 8 points

Soit la fonction f définie sur par .

1)      Déterminer les réels a, b et c tels que l'on puisse écrire .

2)      Etudier les limites de f aux bornes de son ensemble de définition.

3)      Montrer que f admet la droite d'équation  comme asymptote en .

4)      Etudier les variations de f et dresser son tableau de variations.

5)      Calculer les coordonnées des points d'intersection de C_f avec l'axe des abscisses.

6)      Déterminer l'équation de la tangente T à C_f en .

7)      Construire la courbe représentative C_f de la fonction f, ses asymptotes et T.

Exercice n°3 : 5 points

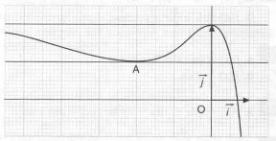La figure ci contre est la représentation graphique d'une fonction h.

1)      Déterminer graphiquement l'ensemble de définition de h.

2)      Déterminer graphiquement les limites suggérées aux bornes de l'ensemble de définition.

3)      Déterminer l'existence d'asymptote(s) ainsi que leur(s) équation(s).

4)      Déterminer le signe de la fonction dérivée.

5)      Dresser le tableau de variation de h.

6)      Résoudre graphiquement l'équation .

7)      Résoudre graphiquement .

8)      Déterminer le nombre de solutions de l'équation  en fonction de .