Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

DEVOIR SURVEILLE N�12
Cliquez ici pour obtenir le document au format Word97 compressé avec winzip.

R�daction et pr�sentation 4 points

Exercice n�1 : 3,5 points

1) D�velopper et r�duire A.

2) Calculer A pour

3) Recopier et compl�ter si possible :

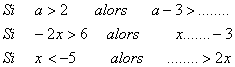
Exercice n�2 : 4 points

1)      Ecrire sous forme d'une fraction irr�ductible en d�taillant les calculs :

2)      Calculer en d�taillant les calculs :

3)      Soit .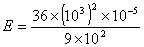

Ecrire E en notation scientifique et en notation d�cimale.

Exercice n�3 : 2,5 points

Le 7 novembre 1998, au retour du second voyage historique de John Glenn dans l'espace, la navette spatiale Discovery avait parcouru 5,8 millions de kilom�tres.

Cette mission ayant dur� 8 jours et 22 heures, calculer la vitesse moyenne en km/h de la navette.

On donnera le r�sultat en �criture d�cimale arrondie au km/h puis en �criture scientifique.

Exercice n�4 : 3 points

Une compagnie d'assurances propose � Monsieur Durand d'assurer son v�hicule.

Le montant de la prime annuelle d'assurances est de 3250 F. Comme Monsieur Durand utilise son v�hicule dans le cadre professionnel, son employeur participe aux frais d'assurances en lui versant une indemnit� annuelle de 1 170 F.

1) Quel pourcentage de la prime annuelle d'assurances la participation de l'employeur repr�sente-t-elle ?

2) La compagnie d'assurances accorde � Monsieur Durand un " bonus ", c'est-�-dire une r�duction de 35% sur la prime annuelle d'assurances. Quel est le montant de cette r�duction ?

3) Quel est .le montant restant � la charge de Monsieur Durand ?

Exercice n�5 : 3 points

Michel ramasse des champignons. Apr�s v�rification, il jette un quart de champignons douteux.

Dans le reste, il y a un tiers de girolles, trois septi�mes de pieds de mouton et 15 c�pes. Combien de champignons Michel avait-il ramass� ?

Exercice n�6 : 4 points

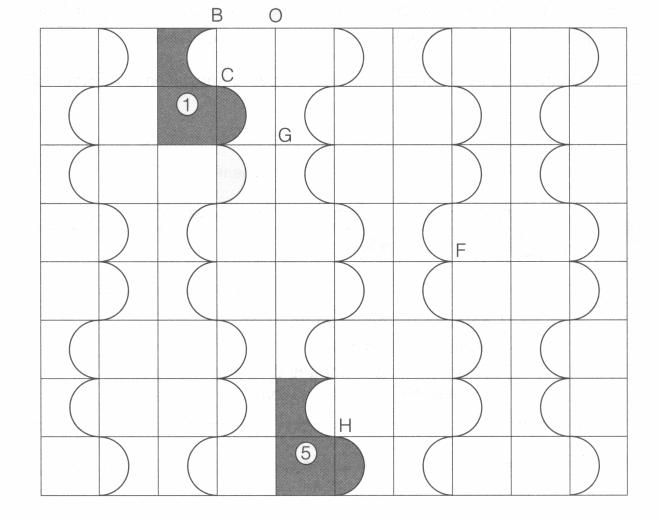
Un dessous de plat a la forme d'un rectangle, recouvert d'un carrelage comme le montre la figure ci-apr�s.

1) a) Hachurer en vert l'image du motif � par la sym�trie axiale d'axe (CG).

��� b) Hachurer en rouge l'image du motif � par la translation qui transforme B en F.

��� c) Hachurer en bleu l'image du motif � par la sym�trie centrale de centre C.

2) Par quelle transformation le motif � a-t-il pour image le motif … ?

Exercice n�7 : 4 points

On consid�re un cercle de diam�tre [AB]. Soit C un point de ce cercle et D le sym�trique de A par rapport au point C. La parall�le � la droite (BC) passant par le point D coupe la droite (AB) en E.

1. R�aliser une figure.

2. Quelle est la nature du triangle ABC ? Justifier.

3. D�montrer que B est le milieu du segment [AE].

4. Quelle est le centre du cercle circonscrit au triangle ADE ?

5. Exprimer l'aire A' du disque de diam�tre [AE] en fonction de l'aire A du disque de diam�tre [AB].

Probl�me : 12 points

On consid�re un triangle �quilat�ral ABC.

Les droites (OA), (OB) et (OC) sont les trois m�diatrices du triangle ABC.

La longueur OB est 6 cm.

La droite (OA) coupe le segment [BC] en A'.

On ne demande pas de reproduire la figure.

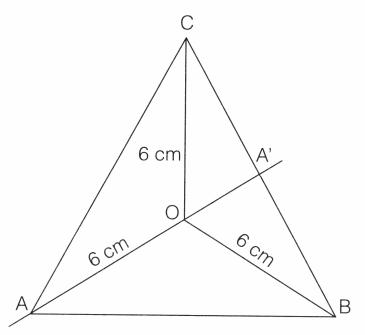1)      Calculer la mesure de l'angle OBA'. En d�duire BOA'.

2)      a) En utilisant le cosinus de l'angle BOA', d�montrer que la longueur du segment [OA'] est 3cm.

����� b) Calculer la longueur BA'.

����� c) En d�duire BC.

3)      Soit E le point du segment [OC] tel que OE = 2 cm.
La parall�le � la droite (BC) passant par le point E coupe le segment [OB] en F.
Calculer les longueurs des segments [OF] et [EF].

4)      Calculer l'aire du triangle COB.

5)      Le cercle circonscrit au triangle ABC coupe la droite (AA') en A et en un autre point not� K.
D�montrer que le quadrilat�re OBKC est un losange.

6)      Calculer l'aire du losange OBKC.