Premiers éléments de géométrie.
I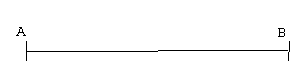 )Segment, demi-droite, droite :
)Segment, demi-droite, droite :
1) Le segment :
Il a pour extrémités les points A et B.
Il se note [AB] ou [BA].
On note sa longueur AB.
Le point M appartient au segment [AB]. On le note M Î [AB].
Cela signifie que le point M est situé entre les points A et B sur la ligne droite passant par A et B.
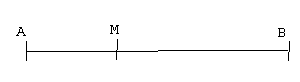
Définition : On appelle le milieu d'un segment [AB], le point de ce segment qui est à égale distance de ses extrémités. (ou équidistant
).
Exemple : I est le milieu de [AB].
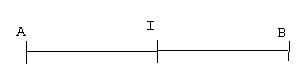 2)Droite, demi-droite :
2)Droite, demi-droite :
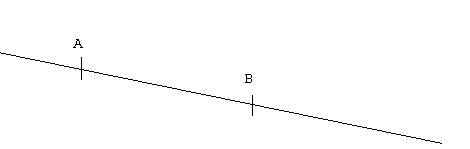
Définition : la ligne droite infinie qui passe par les points A et B est appelée droite (AB).
Définition : la demi droite [AB) est la ligne droite infinie qui part de A et qui va en direction de B.
II) Le cercle
Définition : un cercle est un ensemble de points qui sont à la même distance (équidistants) d'un même point.
Exemple :
|
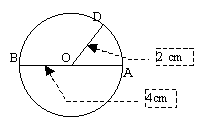
Pour ce cercle, O est le centre,
3 cm est son rayon et 6 cm son
diamètre.
|
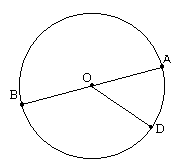
Pour ce cercle, [OA], [OB], [OC] sont des rayons, [AB] est un diamètre.
On dit que les points B et A sont diamétralement opposés.
|
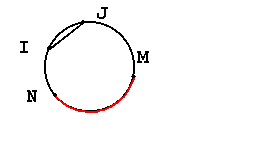
La partie du cercle colorée en rouge est appelée arc de cercle.
On le note : MN .
III) Triangles particuliers :
1)Triangles particuliers :
Définition : un triangle isocèle est un triangle qui possède deux côtés de même longueur.
Définition : un triangle équilatéral est un triangle qui a tous ses côtés de même longueur.
Exemple :
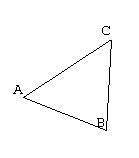
Ce triangle est un triangle isocèle car AB = BC.
On dit qu'il est isocèle en B.
B est son sommet principal et AC est sa base.
IV) Angles, utilisation du rapporteur :
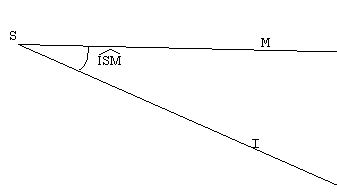
1) Angles : S est le sommet de l'angle.
[SI) et [SJ) sont les côtés de l'angle.
On note cet angle : ISM .
Sa valeur est exprimée en degrés
(de 0° à 180°).
2) Utilisation du rapporteur :
Placer le centre du rapporteur sur le sommet de l'angle puis, placer le 0 du rapporteur sur un côté de l'angle et enfin lire sur le deuxième côté la valeur de l'angle.
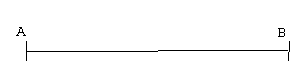 )Segment, demi-droite, droite :
)Segment, demi-droite, droite :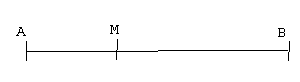

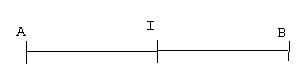 2)Droite, demi-droite :
2)Droite, demi-droite :



