TES 1, 2, 3 devoir commun du 31/01/2 010 durée : 3 heures

NOM :

Accès direct à :
télécharger le document au format open office

Les calculatrices sont autorisées

Exercice 1 5 points

Pour chacune des cinq propositions ci-dessous, indiquer si la proposition est vraie ou fausse en justifiant la réponse faite.

  1. La fonction est la fonction dérivée de la fonction .

  2. L'équation a une autre solution que 1.

  3. Si alors .

  4. L'ensemble des solutions dans R de l'équation est .

  5. La limite quand x tend vers 1, x < 1, de la fonction 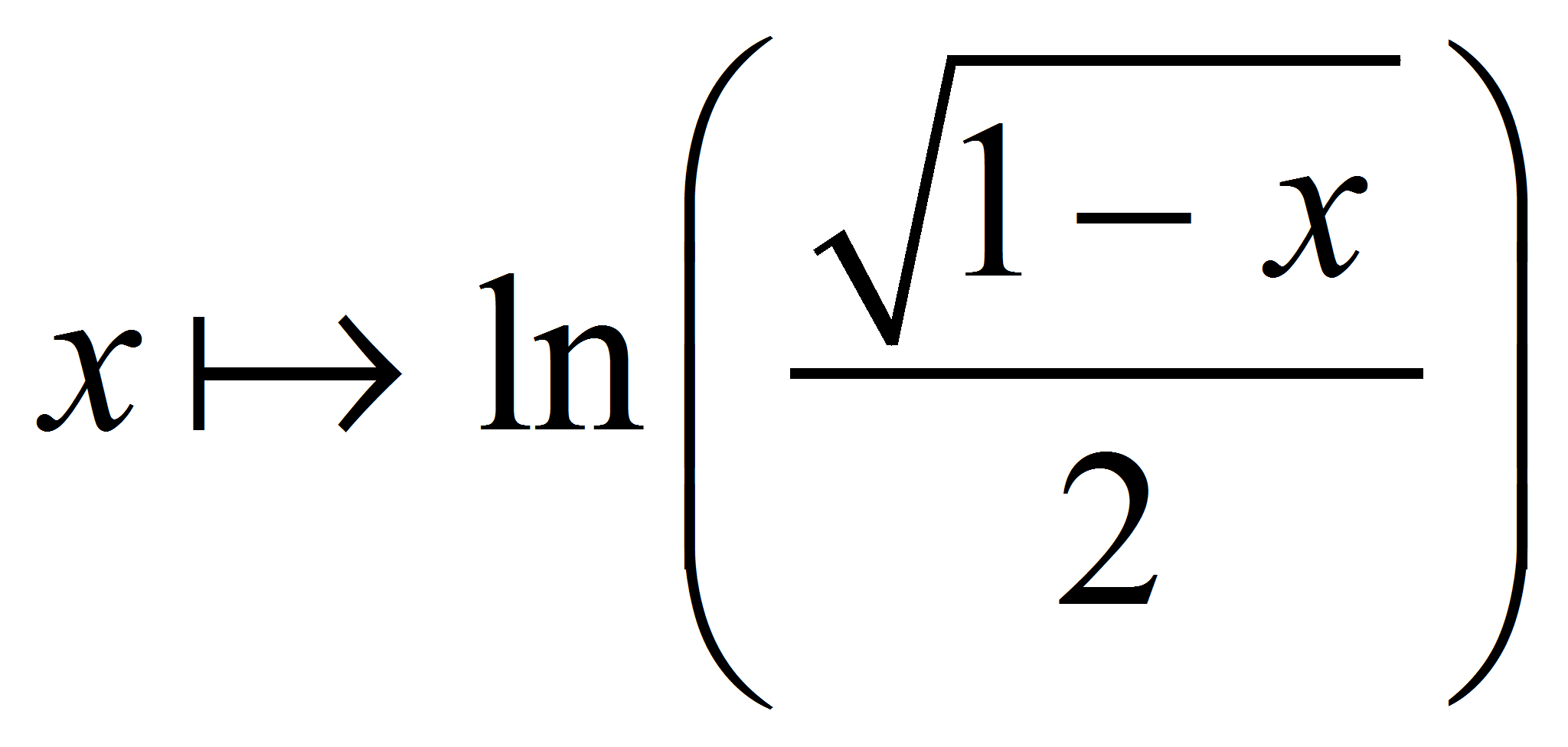est 0.

Exercice 2 5 points

On donne ci-dessous la proportion, en pourcentage, du nombre d'enfants nés hors mariage en France métropolitaine.

Année ai

1 980

1 985

1 990

1 995

2 000

2 003

Proportion yi

11,4

19,6

30,1

37,6

42,6

45,2

On souhaite effectuer un ajustement de cette série statistique de la proportion en fonction de l'année.

  1. a) Construire le nuage de points de coordonnées (ai , yi) dans le plan muni du repère orthogonal suivant
    - sur l'axe des abscisses, on placera 1 980 à l'origine et on prendra comme unité 0,5 cm,
    - sur l'axe des ordonnées, on placera 10 à l'origine et on prendra comme unité 0,5 cm.
    b) Un ajustement affine semble-t-il adapté ?

  2. On note a l'année et y la proportion, on pose et
    a) Compléter le tableau suivant :

Année ai

1 980

1 985

1 990

1 995

2 000

2 003

xi = ai – 1 950

30

          

3,401

          

yi

11,4

          


On donnera pour t des valeurs arrondies au millième
b) Exprimer y en en fonction de t par une régression linéaire en utilisant la méthode des
moindres carrés. On arrondira les coefficients au dixième.
c) En déduire la relation : .
d) Quel pourcentage du nombre d'enfants nés hors mariage (arrondi à 1 %), peut-on
prévoir en 2 010 en utilisant cet ajustement ?
e) A partir de quelle année peut-on prévoir que la proportion du nombre d'enfants nés
hors mariage sera-t-elle supérieure à 60 % ?

Exercice 3 5 points

Dans un lycée général et technologique, il y a 1 400 lycéens : des élèves de seconde, première et terminale et des étudiants en section de technicien supérieur (STS).

Pour pouvoir disposer des collections de manuels scolaires, tous les lycéens doivent adhérer à la coopérative scolaire et payer une location annuelle de 50 € pour les élèves et 60 € pour les étudiants.
Sur l'ensemble des adhérents à la coopérative scolaire, 62.5 % sont des élèves de seconde, première et terminale. Les autres sont les étudiants de STS.

Depuis quelques années, les élèves de seconde, première et terminale disposent de chèque-livre avec lesquels ils peuvent régler cette location :

Les parties I et II sont indépendantes.

Partie I

Les 1 400 lycéens, élèves comme étudiants, adhérent à cette coopérative.

  1. Calculer le montant des versements effectués par chèque bancaire.

  2. Calculer le pourcentage du montant total des locations que cette somme représente.

Partie II

On prend au hasard la fiche d'un adhérent à la coopérative scolaire parmi les 1 400 fiches.

On note

  1. Traduire à l'aide d'un arbre pondéré la situation décrite ci-dessus.

  2. a) Calculer la probabilité que l'adhérent soit un élève ayant payé sa location à l'aide de chèque-livre.
    b) Calculer la probabilité que l'adhérent soit un étudiant en STS ayant payé sa location à l'aide d'un chèque bancaire.
    c) Démontrer que la probabilité que l'adhérent ait payé par chèque bancaire est 0,71.

  3. Un adhérent a payé par chèque bancaire. Calculer la probabilité que ce soit un élève.

Exercice 4 5 points

On admettra que toutes les fonctions considérées dans cet exercice sont dérivables sur l'intervalle

]0 ; + 8[.

Soit la fonction f définie sur l'intervalle ]0 ; + 8[ par : .

La figure ci-dessous donne la courbe représentative (Cf ) de la fonction f dans un repère orthonormal .

La courbe (Cf ) coupe l'axe des abscisses en A(1 ; 0) et en B.
La tangente en C à la courbe (Cf ) est parallèle à l'axe des abscisses et la tangente en A à la courbe (Cf ) coupe l'axe des ordonnés en D.

  1. Déterminer l'abscisse du point B (la valeur exacte est demandée)

  2. Calculer la limite de f en 0 et en + 8.

  3. On note f ' la fonction dérivée de f sur ]0 ; + 8[.
    a) Démontrer que pour tout réel     x de l'intervalle ]0 ; + 8[, .
    c) Justifier le sens de variation de la fonction     f sur l'intervalle ]0 ; + 8[.
    b) Déterminer les coordonnées du point C et l'ordonnée du point D (les valeurs exactes sont demandées).

  4. a) Soit g la fonction définie sur l'intervalle ]0 ; + 8[ par : .
    Démontrer que     g est une primitive de f sur l'intervalle ]0 ; + 8[.
    b) En déduire la primitive     F de la fonction f sur l'intervalle ]0 ; + 8[ s' annulant pour . Donner le résultat sous une forme simplifiée.