Devoir Surveillé n°

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

télécharger le document au format open office

Exercice n°1:

Soit ABC un triangle rectangle isocèle en A.Soit I le milieu de [BC]. M est un point du segment [BC] disctinct de B, de C et de I. Soit J et K les pieds des hauteurs issue de M dans les triangles AMB et AMC.

1. Démontrer que les droites (IJ) et (IK) sont perpendiculaires.

2. En déduire que les points M, I, J et K appartiennent à un même cercle dont on précisera le centre.

3. Soit A' l'image de A par la symétrie orthogonale d'axe (BC),
   Démontrer que les droites (AM') et (JK) sont perpendiculaires.

4. Quelle est la nature du quadrilatère ABA'C?

5. Soit L et N les symétriques du point M respectivement par rapport aux droites (AB) et (AC).
   Démontrer que les points L, A et N sont alignés et que A est le milieu de [LN].

Exercice n°2:

1. Ecrire sous la forme d’un quotient dont le dénominateur est un nombre entier.

2. Calculer et donner le résultat sous forme d'une fraction irréductible: 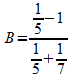et .

3. Donner une valeur approchée au centième de .

4. 
   En utilisant la décomposition en facteurs premiers, donner le PGCD de et de .

Exercice n°4: BONUS

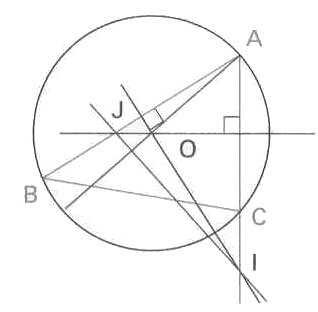
Soit ABC un triangle et O le centre de son cercle circonscrit.

On appelle I le point d'intersection de la médiatrice du segment [AB] et de la droite (AC), et J le point d'intersection de la médiatrice du segment [AC] et de la droite (AB).

Démontrer que les droites (AO) et (IJ) sont perpendiculaires.

Exercice en plus

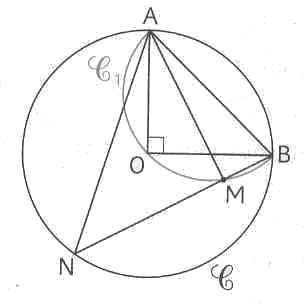
[OA] et [OB] sont deux rayons perpendiculaires d'un cercle C de centre O. C₁ est le demi-cercle de diamètre [AB] passant par O. M est un point de C₁ distinct de A, B et O. La droite (BM) recoupe C en N.

1. Pourquoi ?

2. Démontrer que le triangle AMN est rectangle isocèle.