Devoir Surveillé n°3 (2heures)

Accès direct à :
télécharger le document au format open office

Le barème est donné à titre indicatif

Exercice n°1: 4 points (1 point par réponse juste -0,5 par réponse fausse).

QCM : Choisir la (ou les) réponse(s) correcte(s).

  1. Soit f une fonction définie et dérivable sur [-4 ; 4].
    La courbe ci-contre représente la fonction f ' dérivée de f.

    A .
    B f admet un etremum en .
    C f est décroissante sur [1 ; + ∞ [.
    D La tangente à la courbe représentative de f au point d'abscisse 1 a pour coefficient directeur 2.
    E La courbe de f admet deux tangentes horizontales.

 

  1. Soit g la fonction définie par : pour et . Alors :
    A pour tout et
    B g est croissante sur ]2 ; + ∞ [.
    C g admet un extremum relatif en .
    D il existe des réels a et b tels que pour tout et, .

3) Soit h la fonction définie sur par :

A
B
C
D
E

4) La fonction f dérivable sur est représentée par la courbe dessinée ci-contre. Alors :

A f ' est positive sur [-1 ; 2 ].
B f ' est croissante sur [-1 ; 2 ].
C f ' est décroissante sur [-1 ; 4].
D peut -être un polynôme de degré 3.

 

Exercice n°2:6 points

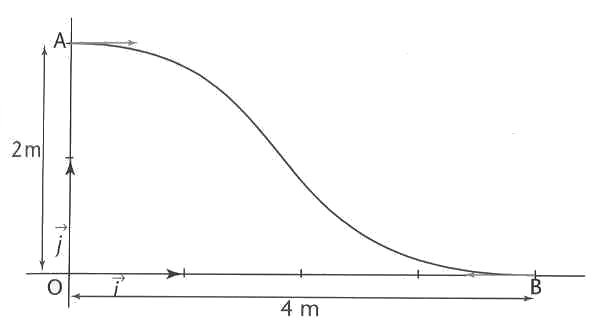
On veut réaliser un toboggan pour les enfants, qui se termine en pente douce.

Il doit donc vérifier les conditions suivantes :

  1. Il doit avoir une tangente en A parallèle au sol.

  2. Il doit être tangent au sol au point B.

Les coordonnées de A sont donc (0 ; 2) celles de B sont (4 ; 0).

On donne le croquis ci-contre.

Le but du problème est de trouver des fonctions dont les courbes représentatives ont l'allure du toboggan et vérifient les conditions de l'énoncé.

  1. Une fonction polynôme du premier degré peut-elle convenir? Expliquer pourquoi.

  2. On décide de donner au toboggan, un profil correspondant à la courbe représentative d'une fonction polynôme P de degré 3 dans un repère avec : .
    a) Trouver a, b, c et d pour que P vérifie les conditions données.
    b) On considère la fonction h définie sur [0 ; 4] par : .
    Etudier les variations de h et donner son tableau de variations.
    c) Calculer la pente maximale (c'est à dire le maximum de ) du toboggan dans ce cas.
    d) Donner l'équation de la tangente à Ch au point d'abscisse 2.

Exercice n°3:2 points

Soient et deux vecteurs du plan tels que et .

  1. Calculer .

  2. Soient A, B, C trois points du plan tels que et . Donner une valeur approchée de .

Exercice n°4: 6,5 points

PARTIE A :Question de cours : 1,5 points
Dans un repère orthonormal du plan, pour deux vecteurs quelconques et ,
démontrer que .

PARTIE B :

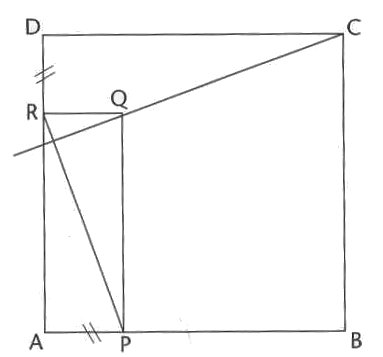
On considère un carré ABCD. On construit un rectangle APQR tel que , et .

On veut démonter que les droites (CQ) et (RP) sont perpendiculaires.

  1. 1ère méthode : 2,5 points
    a) Justifier l'égalité .
    b) Conclure.

  2. 2ème méthode : 2,5 points

    On considère le repère et on pose AP = x.
    a) Donner les coordonnées de C, Q, P et R. On justifiera un minimum.
    b) En déduire .
    c) Conclure.

Exercice n°5: 1,5 points + bonus Les proportions d'une casserole économique.

Vous êtes-vous demandé pourquoi la hauteur d'une casserole est approximativement égale à son rayon quelle que soit sa contenance?

Pour répondre à cette question, on se propose de résoudre le problème suivant :

Comment fabriquer une casserole de volume V donné avec le moins de métal possible?

On suppose que le prix de revient du manche ne dépend pas des dimensions de la casserole.

L'unité est le centimètre. On note x le rayon du cercle du fond, h la hauteur et A l'aire totale égale à l'aire latérale plus l'aire du fond.

  1. Question préliminaire : 1,5 points
    Etudier les variations sur ]0 ; +     ∞[ de la fonction .

  2. a) Démontrer que .
    b) Démontrer que     .

  3. En utilisant les questions 1) et 2), conclure en montrant que h = x.

Accès direct à :
télécharger le document au format open office