DEVOIR SURVEILLE N°2 2h

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

télécharger le document au format open office

Exercice n°1 : 5 points

f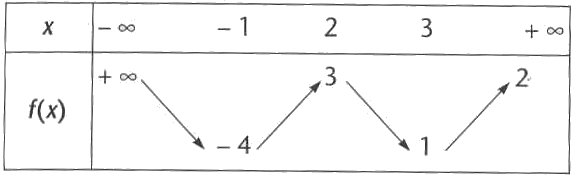
est une fonction définie et dérivable sur dont voici le tableau de variation.

C est la courbe représentative de f dans un repère.

Répondre par Vrai ou Faux aux affirmations suivantes en justifiant.

1. Pour tout réel x, .

2. L'équation admet au moins une solution dans .

3. L'équation admet une unique solution dans .

4. La tangente à la courbe C au point d'abscisse 2 est parallèle à la droite d'équation .

5. .

Exercice n°2 : 7 points

On considère la fonction h définie sur par : et H sa courbe représentative dans un repère.

1. a) Etudier la limite de h en –2 En déduire une asymptote à H.
   b) Etudier la limite de h en .
   c) Vérifier que pour tout x>-2 , . En déduire une asymptote à H.

2. a) Calculer et vérifier que .
   b) Dresser le tableau de variation de h.

Exercice n°3 : 8 points

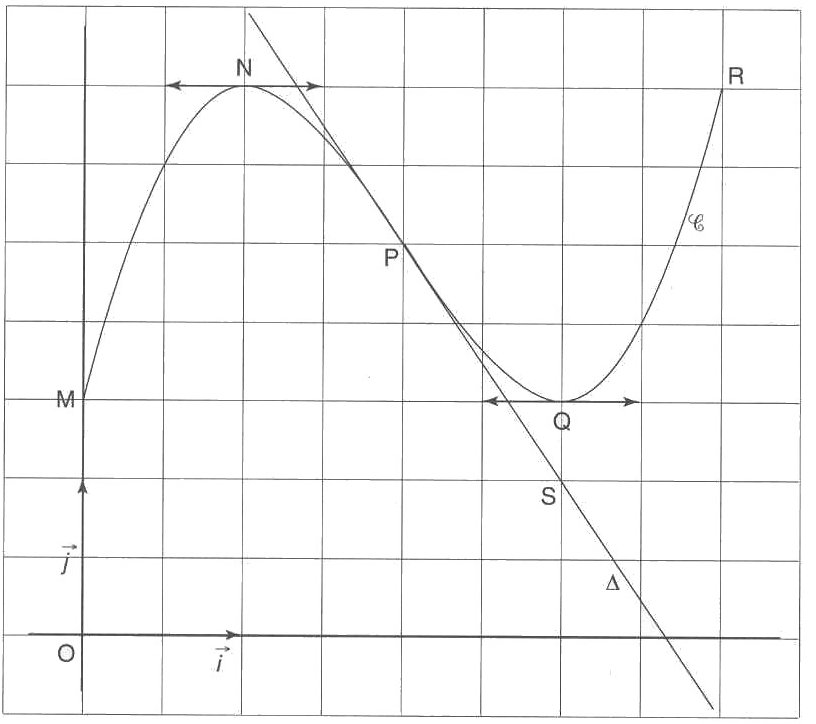
Soit f la fonction définie et dérivable sur l'intervalle [0; 4] dont la représentation graphique, dans un repère orthonormal est la courbe C sur la feuille jointe. Les points M, N, P, Q et R appartiennent à C.
Les coordonnées de M sont , celles de N sont , celles de P sont , celles de Q sont et celles de R sont .

La courbe C admet en chacun des points N et Q une tangente parallèle à l'axe des abscisses.

La droite est la tangente à la courbe C au point P; elle passe par le point S de coordonnées (3; 1).

1. a) Donner , et .
   b) Déterminer une équation de la droite .

2. a) Déterminer à l'aide du graphique le nombre de solutions de l'équation f (x) = 3 sur l'intervalle [0 ; 4].
   b) Tracer la droite d'équation dans le repère ci-dessous puis, à l'aide du graphique, résoudre graphiquement l'inéquation .

3. La fonction f est la dérivée d'une fonction F définie sur l'intervalle [0 ; 4].
   En justifiant la réponse, donner le sens de variation de F.

4. Soit g la fonction définie sur l'intervalle [0; 4] par .
   a) Donner le tableau de variations de f.
   b) En déduire le tableau de variations de g.

 Bonnes vacances 

Nom ………………………………….Prénom…………………………………….

Nom ………………………………….Prénom…………………………………….