DEVOIR SURVEILLE 2h

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

télécharger le document au format open office

La rédaction entrera dans une part importante de la notation.

Exercice n°1 : 3 points

On considère la fonction f définie sur par f(x) = 3(x + 1)² -27.

1. a) Développer l'expression de f(x).
   b) Factoriser le plus possible f(x).

2. a)Étudier le sens de variation de la fonction f sur chacun des intervalles et .
   b) Etablir le tableau de variation de f.
   c) Vérifier que cette fonction possède un minimum sur .
   Quel est-il ? En quelle valeur est-il atteint ?

3. En utilisant l'une des trois formes de f(x) qui vous semble la plus appropriée :
   a) déterminer le ou les antécédents de 0 et de -9.
   b) déterminer l'image de –1 et de .

Exercice n°2 : 2,5 points

1. Résoudre l’inéquation .

2. Résoudre dans l’inéquation .

3. En utilisant la parabole d’équation y = x², résoudre .

Exercice n°3 : 3 points

Soit un repère du plan. On fera une figure que l’on complètera au fur et à mesure de l’exercice.

Soit les points , et .

1. Déterminer les coordonnées du point D tel que ABCD soit un parallélogramme.

2. Déterminer une équation de la droite (AC).

3. Déterminer les coordonnées de E, symétrique de D par rapport à C.

4. Déterminer les coordonnées du point F de la droite (AC) d’abscisse –1.

5. Donner l’équation réduite de la droite (DF).

6. Soit (d) la droite d’équation .
   Donner les coordonnées du point d’intersection de (d) et de (DF) (si il existe !).

Exercice n°4 : 1,5 points

Placer sur le cercle trigonométrique les points A, B, C, D, E et F associés aux réels : .

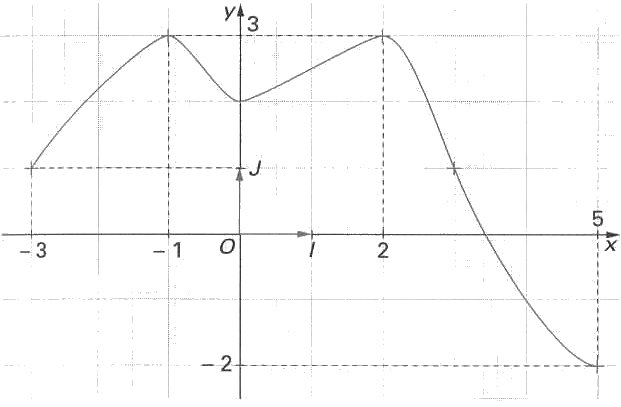
Exercice n°5 : 2 points

On considère la courbe ci-contre, représentant une fonction f dans le repère (O, I, J).

1. Donner le tableau de variation de f.

2. Résoudre graphiquement, en expliquant la méthode, l’inéquation : .

Exercice n°6 : 3 points

E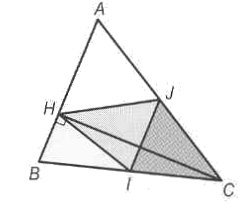
xercice n°7 : 2 points

Dans un triangle ABC, on note H le pied de la hauteur issue de C,
I le milieu de [BC] et J celui de [AC].

Il s'agit de prouver que les triangles ABC et HIJ sont semblables.

1. Prouver que les triangles IJC et IJH sont isométriques.

2. Prouver que IJC et BAC sont semblables.

3. Conclure.

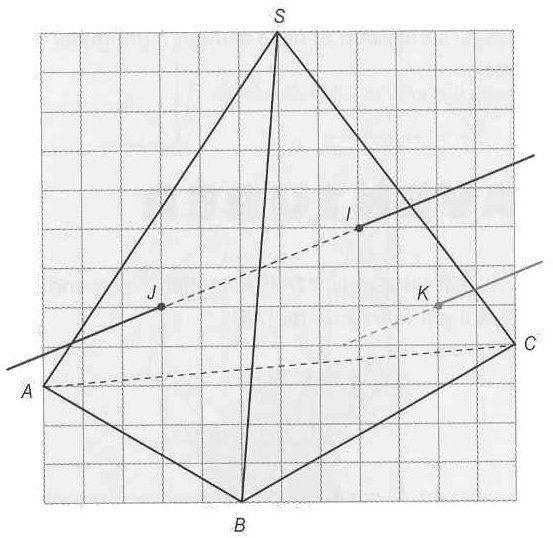
Exercice n°8 : 3points

Soit un tétraèdre SABC, deux points I et K de la face SBC et un point I de la face SAB.

La parallèle à (IJ) passant par K recoupe l'une des faces du tétraèdre en un point L.

On veut construire le point L.

1. Montrer que le point L est un point du plan P déterminé par les points I, J, K.

2. Construire l'intersection de P et de la face SBC.

3. Construire l'intersection de P et de la face SAB.

4. Construire l'intersection de P et de la face ABC.

5. Construire L.

C'est le dernier DS !!

 Bonnes vacances 