DEVOIR SURVEILLE N°1

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

télécharger le document au format open office

Exercice n°1 : Question de cours. 3points

Soient f et g deux fonctions définies sur les intervalles respectifs I et J de telle sorte que existe.

On suppose que f est strictement croissante sur I et que g est strictement décroissante sur J.
Démontrer que est strictement décroissante sur J.

E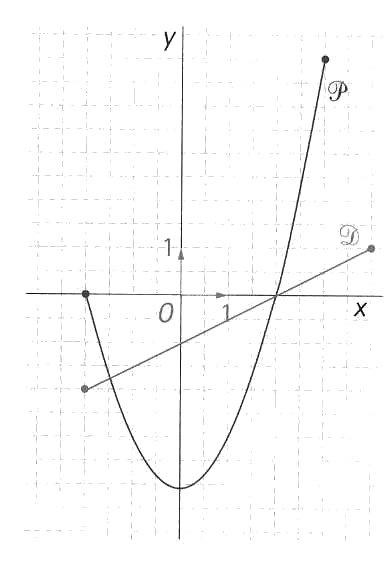 xercice n°2 : 8points

On a représenté ci-contre les courbes :

D d’équation et P d’équation .

1. Quels sont les ensembles de définition de u ? de v ?

2. Quel est l’ensemble des valeurs de  ?

3. a) Pourquoi peut-on définir la fonction  ?
   b) Trouver .
   c) Etudier les variations de f sur [-2 ; 2] et sur [2 ; 4].

Exercice n°3 : 9 points

Soit la fonction h définie sur par : .

1. Montrer que .

2. Etudier les variations de la fonction g : sur .

3. Exprimer h comme une composée faisant intervenir g.

4. En déduire les variations de h.

5. Encadrer h pour .

6. On se place dans un repère .
   Comment passe-t-on de la courbe représentative de la fonction carrée à la courbe représentative de la fonction g?

DEVOIR SURVEILLE N°1
Correction

Exercice n°1 : Questions de cours 3 points

Soient f et g deux fonctions définies sur les intervalles respectifs I et J de telle sorte que existe.

On suppose que f est croissante sur I et que g est décroissante sur J.
Démontrer que est décroissante sur J.
Soit a et b deux nombres réels de l'intervalle J tels que

a < b

car g est décroissante sur J

car f est croissante sur I.

E xercice n°2 : 8 points

On a représenté ci-contre les courbes :

D d’équation et P d’équation .

1. Quels sont les ensembles de définition de u ? de v ?

2. Quels est l’ensemble des valeurs de  ?

3. a) Pourquoi peut-on définir la fonction  ?
   b) Trouver .
   c) Etudier les variations de f sur [-2 ; 2] et sur [2 ; 4].

1. Du=[-2;4] Dv=[-2;3] ce sont les abscisses des points de D, respectivement P .

2. L'ensemble des valeurs de est l'intervalle : [-2;1]. Ce sont les ordonnées des points de D.

3. a) on peut définir car est inclus dans l'intervalle Dv=[-2;3].
   b) (u(-2) c'est l'ordonnée du points de D d'abscisse –2.
   De même .
   c) u est croissante de [-2 ; 2] sur [-2;0] et v est décroissante sur [-2;0]. Donc par composée, est décroissante sur [-2 ; 2].

Exercice n°3 : 9 points

Soit la fonction h définie sur par : .

1. Montrer que .
   

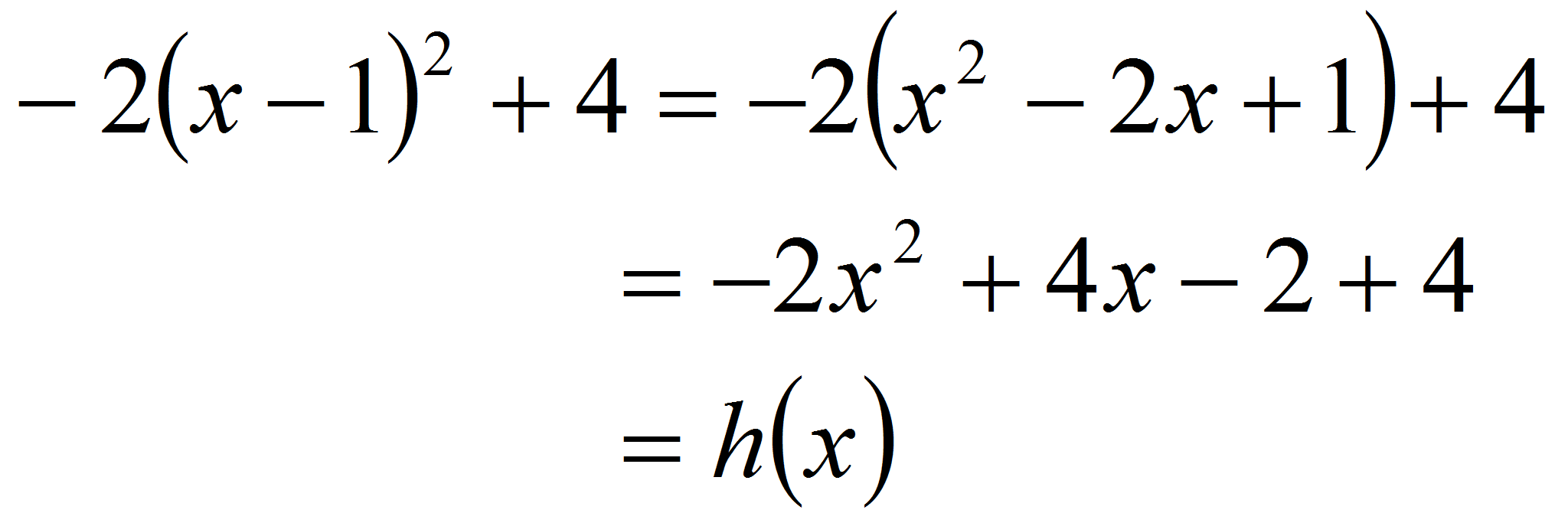
2. Etudier les variations de la fonction g : sur .
   g est la composée de la fonction carrée et de la fonction affine : .
   Cette dernière étant croissante sur , on en déduit que la fonction g est strictement croissante sur et strictement décroissante sur .

3. Exprimer h comme une composée faisant intervenir g.
   h=vg avec v(x) = -2x+4.

4. En déduire les variations de h.
   h est décroissante sur et croissante sur (les variations sont inversées par rapport à g, car v est strictement décroissante.

5. Encadrer h pour .
   ( car 4 est le maximum, c'est h(1) et g(-2) = g(4) = -14)

6. Comment passe-t-on de la courbe représentative de la fonction carrée à la courbe représentative de la fonction g?
   On passe de la courbe représentative de la fonction carrée à la courbe représentative de la fonction g par une translation de vecteur .