Exercice 1 :
Soit f la fonction définie par : 
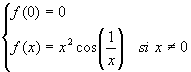
a) Calculer la limite de f en 0.
b) La fonction f est-elle continue en 0 ? sur lR ?
Exercice 2 :
On considère la fonction f définie sur lR par
et on note (C) sa courbe représentative
dans un repère orthonormal 
(unité : 1 cm)
1. On pose 
a)
Etudier le sens de variation de g, et montrer que l’équation 
admet sur lR une unique solution 
dont on donnera un encadrement d’amplitude 0,1.
b)
Préciser le signe de 
selon les valeurs de x.
2.
a) Calculer 
et étudier le sens de variation de f.
b) Etudier les limites de f en 
et en 
, puis dresser le tableau de variation de f.
3.
a) Montrer qu’il existe quatre réels a, b, c
et d tels que 
.
b) En déduire que (C) admet une asymptote oblique 
, et étudier la position de (C) par rapport
à 
. Vérifier en particulier que (C) rencontre
en un unique point A .
4.
Déterminer les abscisses des point B et B’ de (C) admettant
une tangente parallèle à la droite 
.
5.
a) Vérifier que 
; en déduire une valeur approchée de 
.
c) Tracer
et (C) en plaçant les points A, B et B’,
ainsi que les trois points I, J et K d’abscisses respectives 1 , 2 et –1 avec
leurs tangentes.
Pour
contacter le webmaster 
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.
Exercice 3 :
Dans tout l’exercice, n désigne un entier naturel de fn
la fonction définie par 
.
1. Déterminer l’ensemble de définition de fn et étudier sa continuité, sa dérivabilité.
2.
Déterminer l’unique élément an de [0 ; 1[
tel que 
pour 
.
3.
Donner le tableau de variation de fn pour 
, en distinguant les cas n pair et n
impair.
4. Représenter dans un même repère orthonormal les fonctions f0, f1 et f2.