DEVOIR SURVEILLE

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

EXERCICE 1   : 7 points

Le plan est rapporté à un repère orthonormal . On considère la fonction f définie sur l'intervalle  par .

1)      Vérifier que la fonction h, définie par , est une primitive de la fonction logarithme népérien sur .

2)      On pose  et .
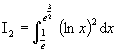a) Calculer I₁.
b) En utilisant une intégration par parties, montrer que .
c) Calculer 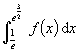. En déduire l’aire de l’ensemble des points  du plan tels que  et .

EXERCICE 2 : 13 points

L'espace est rapporté à. un repère orthonormal . On étudie le tétraèdre OABC, où les points A, B et C sont définis par leurs coordonnées : A(0 ; 0 ; 2), B(  ; 1 ; 0) et C( ; -1 ; 0).

Soit J le milieu de l'arête [BC]. Le point N est un point mobile du segment [OJ]. On appelle (P) le plan passant par le point N et orthogonal à la droite (OJ).

1)      Faire une figure représentant le repère et le tétraèdre.

2)      On pose t = ON. Vérifier que t appartient à l'intervalle [0 ; ].

3)      On se propose de déterminer la nature de la section plane du tétraèdre OABC par le plan (P).
Le plan (P) coupe :
-l'arête [OC] au point R ;
-l'arête [AC] au point S ;
-l'arête [AB] au point T ;
-l'arête [OB] au point U .
a) Démontrer que les droites (ST), (BC) et (RU) sont parallèles.
    On admettra de même que les droites (RS), (OA) et (TU) sont parallèles.
b) Démontrer que le quadrilatère RSTU est un rectangle.
c) Déterminer avec soin les dimensions du rectangle RSTU en fonction du nombre réel t (on précisera en particulier les différents triangles dans lesquels sont menés les calculs ).

4)      Soit S(t) l'aire de la section plane définie à la question 3).
Démontrer que .

5)      On rappelle que le volume V du tétraèdre OABC est égal à l'intégrale .
Calculer V.