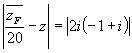DEVOIR SURVEILLE N°2

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

Exercice n°1 : (11 points)

On considère la fonction f définie sur  par .

On note C la courbe représentative de f dans un repère orthonormal  (unité graphique 2 cm).

1)      a) Déterminer les limites de f aux bornes de son domaine de définition.
b) Montrer que la droite D d’équation  est asymptote à C.
Etudier la position de C par rapport à D.

2)      Montrer que f est dérivable sur  et calculer .

3)      Soit u la fonction définie sur  par .
a) Etudier le sens de variation de u.
b) Montrer que l’équation  possède une solution unique  dans l’intervalle .
Déterminer une valeur décimale approchée par excès de  à 10^-2 près.
c) Déterminer le signe de  suivant les valeurs de x.

4)      Etudier le sens de variation de f puis dresser son tableau de variation.

5)      Construire C.

Exercice n°2 : (4 points)

Soit les nombres complexes  et . On pose .

1)      Ecrire z₁ et z₂ sous forme trigonométrique.

2)      Déterminer l’écriture algébrique de Z puis son écriture trigonométrique.

3)      En déduire  et

Exercice n°3 : (5 points)

Le plan complexe est muni d’un repère orthonormal direct  d’unité graphique 2 cm.

On désigne par A le point d’affixe , et par  le cercle de centre A et de rayon 1.

Soit B le point d’affixe  et E le point d’affixe .

1)      a) Montrer que B appartient au cercle .
b) Placer B.

2)      a) Déterminer la forme trigonométrique des nombres complexes  et .
b) Placer E.

3)      Soit F d’affixe .
Déterminer et tracer l’ensemble des points M d’affixe z tel que