DEVOIR SURVEILLE T^le S

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

MATHÉMATIQUES

Série : S

Durée du l’épreuve : 3h30

L’utilisation d’une calculatrice n’est pas autorisée.

Ce sujet comporte 4 pages numérotées de 1 à 4.

Le candidat doit traiter les DEUX exercices et le problème.

La qualité de la rédaction, la clarté et la précision des raisonnements entreront pour
une part importante dans l’appréciation des copies.

page 1/4

Tournez la page S.V.P.

EXERCICE 1  (commun à tous les candidats) : 4 points

1)      Pour tout nombre complexe z, on considère .
a) Soit b un nombre réel. Exprimer en fonction de b les parties réelle et imaginaire de .
    En déduire que l’équation  admet deux nombres imaginaires purs comme solution.
b) Montrer qu’il existe deux nombres réels  et , que l’on déterminera, tels que pour tout
     nombre complexe z, .
c) Résoudre dans l’ensemble des nombres complexes l’équation .

2)      Le plan complexe P est rapporté à un repère orthonormal.
a) Placer les points A, B, C et D ayant respectivement pour affixes : , ,  et .
b) Déterminer l’affixe de l’isobarycentre G des points A, B, C et D.
c) Déterminer l’ensemble E des points M du plan tels que : .

Tracer E sur la figure précédente.

EXERCICE 2 (candidats n’ayant pas suivi l’enseignement de spécialité) : 6 points

Le plan complexe est muni d’un repère orthonormal direct   (unité graphique 2 cm).

A tout nombre complexe distinct de 4, on associe le nombre .

On note A le point d’affixe 4 et on considère l’ensemble H des points M du plan, distinct de A et d’affixe z tels que Z soit réel.

On se propose de déterminer et de construire H par deux méthodes différentes.

1)      Méthode algébrique :
a) On pose  et  avec x, y, X et Y des nombres réels.
Exprimez X et Y en fonction de x et y.
b) Ecrire une équation cartésienne de H. Reconnaître la nature de H et caractériser cet ensemble.
c) Construire H.

2)      Méthode géométrique :
On considère le point B d’affixe .
a) Vérifier que  est réel si et seulement si le nombre  est imaginaire pur.
b) Quelles sont les affixes des vecteurs  et  ?
c) En interprétant géométriquement la condition ci-dessus, établir que M appartient à H si et seulement si  et sont orthogonaux.
En déduire la nature de H et caractériser cet ensemble.

page 2/4

EXERCICE 1  (commun à tous les candidats) : 4 points

1)      Pour tout nombre complexe z, on considère .
a) Soit b un nombre réel. Exprimer en fonction de b les parties réelle et imaginaire de .
En déduire que l’équation  admet deux nombres imaginaires purs comme solution.
b) Montrer qu’il existe deux nombres réels  et , que l’on déterminera, tels que pour tout nombre complexe z, .
c) Résoudre dans l’ensemble des nombres complexes l’équation .

2)      Le plan complexe P est rapporté à un repère orthonormal.
a) Placer les points A, B, C et D ayant respectivement pour affixes : , ,  et .
b) Déterminer l’affixe de l’isobarycentre G des points A, B, C et D.
c) Déterminer l’ensemble E des points M du plan tels que : .
Tracer E sur la figure précédente.

EXERCICE 2 (candidats ayant suivi l’enseignement de spécialité) : 6 points

Partie A

Soit N un entier naturel, impair non premier.

On suppose que N = a² - b² où a et b sont deux entiers naturels.

1)      Montrer que a et b n'ont pas la même parité.

2)      Montrer que N peut s'écrire comme produit de deux entiers naturels p et q.

3)      Quelle est la parité de p et de q?

Partie B

On admet que 250507 n 'est pas premier .

On se propose de chercher des couples d'entiers naturels (a; b) vérifiant la relation

(E) : a²- 250507 = b².

1)      Soit X un entier naturel.
a) Donner dans un tableau, les restes possibles de X modulo 9; puis ceux de X² modulo 9.
b) Sachant que a² -250507 = b², déterminer les restes possibles modulo 9 de a² -250507; en déduire les restes possibles modulo 9 de a².
c) Montrer que les restes possibles modulo 9 de a sont 1 et 8.

2)      Justifier que si le couple (a; b) vérifie la relation (E), alors . Montrer qu'il n'existe pas de solution du type (501; b).

3)      On suppose que le couple (a; b) vérifie la relation (E).
a) Démontrer que a est congru à 503 ou à 505 modulo 9.
b) Déterminer le plus petit entier naturel k tel que le couple (505 + 9k ; b) soit solution de (E), puis donner le couple solution correspondant.

Partie C

1)      Déduire des parties précédentes une écriture de 250507 en un produit de deux facteurs.

2)      Les deux facteurs sont-ils premiers entre eux?

3)      Cette écriture est-elle unique ?

page 2/4

PROBLEME (Commun à tous les candidats) : 10 points.

Partie A :

Soient a,b et c des nombres réels.
On définit une fonction g sur  par : .
a) Calculer .
b) Le tableau de variation de g est le suivant :

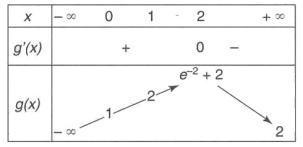
En utilisant les données numériques de ce tableau, trouver a,b et c.

Partie B :

Soit : .

1)      a) Montrer que l’équation  admet une solution unique dans l’intervalle .
    On note  cette solution.
b) Déterminer un encadrement au dixième de .

2)      Etudier le signe de  pour x appartenant à .

Partie C :

Soit f la fonction définie sur  par .

1)      a) Déterminer la limite de f en .
b) Déterminer la limite de f en .

2)      a) Soit  la fonction dérivée de f. Montrer que .
b) Dresser, en le justifiant, le tableau de variation de f sur .

3)      Dans le plan muni d’un repère orthonormal  on appelle C la représentation graphique de f et D la droite d’équation .
a) Démontrer que D est asymptote à C en .
b) Etudier la position de C par rapport à D.

4)      Tracer une ébauche de la courbe et son asymptote.

page 3/4

Données numériques et formules :

page 4/4