DEVOIR SURVEILLE N°15

Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

télécharger le document au format word

Exercice n°1 : 2 points

1)      Décomposer  et  en produit de facteurs premiers.

2)      En déduire une simplification de A.

3)      En déduire l’écriture de B sous la forme ,  et , avec a le plus grand possible.

4)      Déterminer le PGCD (plus grand diviseur commun) et le PPCM (plus petit multpile commun) de C et D
avec  et .

Exercice n°2 : 3 points

1)      Calculer .

2)      Résoudre .

3)      Résoudre .

4)      Résoudre .

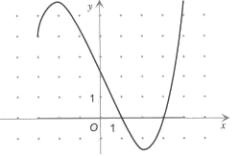
Exercice n°3 : 2 points

Soit f la fonction définie sur  dont la représentation graphique est donnée ci-contre.

1)      Dresser le tableau de variations de f.

2)      Donner l'image de 4 par f.

3)      Donner le(s) antécédent(s) de 2 par f.

4)      On sait que f est définie par l'une des 4 expressions algébriques suivantes :
.

Identifier f en justifiant.

Exercice n°4 : 3 points

Soit un repère (O , I , J) et la fonction f définie sur  par .

1)      Montrer que .

2)      Etudier les variations de f sur  puis sur .

3)      Dresser le tableau de variations de f et en déduire son maximum et en quelle valeur il est atteint.

4)      Recopier et compléter, à l'aide de la calculatrice, le tableau de valeurs suivant :

5)      Placer les points correspondants dans le repère et tracer la courbe représentative de f.

Exercice n°5 : 2 points

Exercice n°6 : 2 points

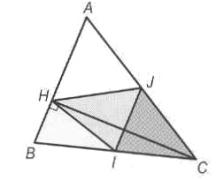
Dans un triangle ABC, on note H le pied de la hauteur issue de C,
I le milieu de [BC] et J celui de [AC].

Il s'agit de prouver que les triangles ABC et HIJ sont semblables.

1)      Prouver que les triangles IJC et IJH sont isométriques.

2)      Prouver que IJC et BAC sont semblables.

3)      Conclure.

Exercice n°7: 3 points

Soit ABC un triangle. Le point A' est le milieu de [BC].

On appelle C' le point de [AB] tel que  et B' le point de [AC] tel que .

Les droites  et  se coupent en E. Les droites  et  se coupent en F.

1)      Prouver, de deux façons différentes, que les droites  et  sont parallèles.

2)      On introduit le repère .
Donner les équations des droites , ,  et  dans ce repère.

3)      Trouver les coordonnées de E et F dans ce repère.

4)      La droite  est-elle parallèle à la droite ?

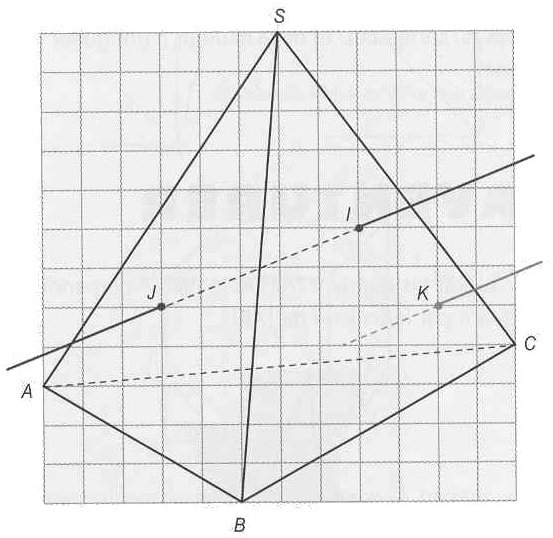
Exercice n°8 : 3points

Soit un tétraèdre SABC, deux points I et K de la face SBC et un point I de la face SAB.

La parallèle à (IJ) passant par K recoupe l'une des faces du tétraèdre en un point L.

On veut construire le point L.

1)      Montrer que le point L est un point du plan P déterminé par les points I, J, K.

2)      Construire l'intersection de P et de la face SBC.

3)      Construire l'intersection de P et de la face SAB.

4)      Construire l'intersection de P et de la face ABC.

5)      Construire L.

C'est le dernier DS !!

J Bonnes vacances J