DEVOIR SURVEILLE N°1
Exercice
n°1 : 4 points
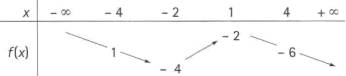
On donne le tableau de variations ci-contre :
Dire si les affirmations suivantes sont vraies ou fausses en justifiant uniquement le 2).
1)
Sur 
, l’équation 
a une solution unique.
2)
Sur 
, l’équation 
a une solution unique.
3)
Sur 
, l’équation 
a deux solutions.
4)
Sur 
, l’équation 
n’a pas de solution.
Exercice n°2 : 16 points
Soit la fonction g définie sur 
par 
et la fonction h définie sur 
par : 
.
On appellera Cg et Cf leur courbe représentative
respective dans un repère 
d’unité graphique 3 cm en abscisse et 0,5 cm en
ordonnée.
Partie A :
1)
Etudier la limite de g en 
puis sa limite en 
.
2) Etudier la limite de g en 2. En donner une interprétation graphique.
3)
a) Trouver les nombres réels a, b et c tels
que 
.
b) En déduire que la droite D d’équation 
est asymptote à Cg en 
.
4) Etudier la position relative de D et de Cg.
Partie B :
1) Etudier les variations de h, puis donner son tableau de variations.
2)
Donner le nombre de solutions de l’équation 
sur 
.
3) Donner un encadrement à 10-1 près de la ou des solutions.
Partie C :
1) Tracer D, Ch , Cg et les asymptotes de la partie A.
2)
Résoudre graphiquement l’inéquation :
.
3)
Trouver graphiquement, en fonction
de k, le nombre de solutions de l’équation 
.
Pour
contacter le webmaster 
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.