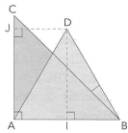
I est le milieu de [AB] et J le projeté orthogonal de D sur (AC).
On pose AB = a.
DEVOIR SURVEILLE N°3
Exercice n°1 : 5 points
Dans la figure ci-après, ABC est un triangle
rectangle isocèle, ABD est équilatéral.
I est le milieu de [AB] et J le projeté orthogonal de D
sur (AC).
On pose AB = a.
1)
![]() a) Calculer, en fonction
de a,
a) Calculer, en fonction
de a, ![]() et
et ![]() .
.
b) En déduire que ![]() .
.
2) Calculer une mesure en radians de l' angle DBC.
3)
Déduire des résultats précédents
que ![]() .
.
4)
On considère le repère orthonormé ![]() .
.
a) Déterminer les coordonnées de ![]() et
et ![]() .
.
b) En déduire ![]() . Vérifier avec le résultat du 1)b).
. Vérifier avec le résultat du 1)b).
Exercice n°2 : 3,5 points
Une cagnotte du loto s’élève à 30 000 € et doit être partagée, à parts égales, entre les gagnants. S’il y avait eu quatre gagnants de moins, chacun aurait reçu 1250 € de plus.
Combien y a-t-il de gagnants et quelle est la part de chacun ?
Exercice n°3 : 3 points
Soit ABC un triangle tel que AC =12 cm, AB = 9 cm et BC = 8 cm.
Déterminer et tracer l’ensemble des points M du plan tel que ![]() .
.
Exercice n°4 : 8,5 points
Soit la fonction f définie sur ![]() par
par ![]() .
.
Partie A :
1)
Calculer ![]() .
.
2)
Trouver les nombres réels a,
b et c tels que ![]() .
.
3)
Résoudre ![]() .
.
Partie B :
1)
Dresser le tableau de variations de la fonction g définie
sur ![]() par :
par : ![]() .
.
2)
Vérifier que la droite d’équation ![]() est axe de symétrie de Cg, représentation graphique de g dans un repère
est axe de symétrie de Cg, représentation graphique de g dans un repère
![]() .
.
3) Tracer Cg.
4)
Soit D la droite d’équation ![]() .
.
a) Trouver les coordonnées des points d’intersection de D et de Cg.
b) Vérifier graphiquement.
Partie C :
Soit la fonction h définie sur ![]() * par :
* par : ![]() .
.
1)
Trouver le domaine de définition
de ![]() .
.
2)
Donner l’expression algébrique
de ![]() .
.
3)
En utilisant le tableau de variations
de g, donner celui de ![]() .
.