DEVOIR SURVEILLE N°2
Cliquez ici pour obtenir
le document au format Word compressé avec winzip.
Durée 2h
Exercice : 6 points
1)
Résoudre dans 
l’équation :
.
2)
Résoudre dans 
l’inéquation
: 
.
3)
Soit la fonction h définie
sur 
par :
.
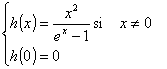Justifier que h est continue en 0.
4)
Résoudre dans 
l’inéquation :
.
Problème : 14 points
Soit f la fonction définie sur 
par
.
On note C la courbe représentative de f dans un repère orthonormal d’unité graphique 2 cm.
A.
Etude d’une fonction auxiliaire :
Soit g la fonction définie
sur 
par :
.
1) Etudier les limites de g en 
et
en 
.
2) Etudier le sens de variation de g.
3) Démontrer que l’équation 
admet
une solution unique notée 
dans
,
puis justifier que 
.
4) En déduire le signe de g.
B.
Etude de f :
1) Etudier les limites de f en 
et
en 
.
2) Etudier les variations de f.
3) Démontrer que 
et
déterminer un encadrement de 
d’amplitude
.
4) Démontrer que la droite 
d’équation
est
asymptote à C en 
.
Etudier la position de C par rapport à 
.
5) Donner une équation de la tangente T à C au point d’abscisse 0.
6) Tracer 
,
T
et C.
On rappelle que pour 
entier naturel : 
Pour
contacter le webmaster 
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.