Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

BACCALAURÉAT GÉNÉRAL BLANC
Cliquez ici pour obtenir le document au format Word compressé avec winzip.

SESSION 2004

MATHÉMATIQUES

Série : S

Durée du l’épreuve : 4h

L’utilisation d’une calculatrice autorisée.

Ce sujet comporte 4 pages numérotées de 1 à 4.

Le candidat doit traiter les DEUX exercices et le problème.

La qualité de la rédaction, la clarté et la précision des raisonnements entreront pour
une part importante dans l’appréciation des copies.

Tournez la page S.V.P.

Exercice n°1 : 5 points.

Les résultats seront donnés sous forme de fractions irréductibles.

Un joueur achète 10 euros un billet permettant de participer à un jeu constitué d'un grattage suivi d'une loterie.

Il gratte une case sur le billet. Il peut alors gagner 100 euros avec une probabilité de  ou bien ne rien gagner.

G désigne l'événement: « le joueur gagne au grattage ».

Il participe ensuite à une loterie avec le même billet. A cette loterie, il peut gagner 100 euros, ou 200 euros, ou bien ne rien gagner.

L₁ désigne l'événement: « Le joueur gagne 100 euros à la loterie ».

L₂ désigne l'événement: « Le joueur gagne 200 euros à la loterie ».

p désigne l'événement: « Le joueur ne gagne rien à la loterie ».

Si le joueur n'a rien gagné au grattage, la probabilité qu'il gagne 100 euros à la loterie est , et la probabilité qu'il gagne 200 euros à la loterie est .

1)        a) Faire un arbre sur lequel on indiquera les renseignements qui précèdent.
b) Calculer la probabilité pour que le joueur ne gagne rien à la loterie, sachant qu'il n'a rien gagné au grattage. Compléter l'arbre obtenu avec cette valeur.
c) Au bout de chaque branche, indiquer le gain algébrique total du joueur, après grattage et loterie, déduction faite du prix du billet.

2)        On note X la variable aléatoire qui représente le gain algébrique total du joueur, après grattage et loterie, déduction faite du prix du billet.
La probabilité de l'événement « X= 90 » est .
La probabilité de l'événement« X= 190 » est .
a) Montrer que la probabilité que le joueur gagne 100 euros à la loterie, sachant qu'il a gagné 100 euros au grattage, est égale à .
b) Calculer la probabilité que le joueur ne gagne rien à la loterie, sachant qu'il a gagné 100 euros au grattage.
c) Déterminer la loi de probabilité de X.
Calculer l'espérance de X. En donner une interprétation.

Tournez la page S.V.P.

Exercice n°2 (candidats n’ayant pas suivi l’enseignement de  spécialité): 5 points

1)        Résoudre dans  l’équation : .

2)        Dans le plan complexe rapporté à un repère orthonormé , d’unité graphique 1 cm, on considère les points A, B, C et P d’affixes respectives :  et le vecteur  d’affixe .
a) Déterminer l’affixe z_Q du point Q, image du point B par la translation t de vecteur .
b) Déterminer l’affixe z_R du point R, image du point P par l’homothétie h de centre C et de rapport .
c) Déterminer l’affixe z_S du point S, image du point P par la rotation r de centre A et d’angle .
d) Placer les points P, Q, R et S.

3)        a) Démontrer que le quadrilatère PQRS est un parallélogramme.
b) Interpréter géométriquemen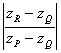t  et .
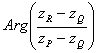c) Calculer 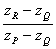. En déduire la nature du quadrilatère PQRS.
d) Justifier que les points P, Q, R et S appartiennent à un même cercle, noté C.
On calculera l’affixe de son centre et son rayon.

4)        La droite  est-elle tangente au cercle C ?.

Tournez la page S.V.P.

Exercice n°2  (candidat ayant suivi l’enseignement de spécialité) : 5 points

n et c étant deux entiers naturels non nuls, le but de l’exercice est de comparer le PGCD de cn et de 2n+1 au PGCD de c et de 2n+1, puis de déterminer selon les valeurs de n, le PGCD des deux nombres A= 3n et
B= 2n+1.

1)      Montrer que n et 2n+1 sont premiers entre eux.

2)      En utilisant le théorème de Bezout, démontrer que pour tout entier naturel c non nul le PGCD de cn et 2n+1 est égal au PGCD de c et 2n+1.

3)      En déduire que le PGCD de A et B est le PGCD de 3 et de (2n+1).

4)      Déterminer le PGCD de 3 et de (2n+1) selon les valeurs de n, en utilisant par exemple, les 3 valeurs possibles du reste dans la division euclidienne de n par 3.

Tournez la page S.V.P.

Problème : 10 points

Le but du problème est l’étude d’une fonction g_k, ou k est un réel fixé qui vérifie : 0<k<e.

Dans la partie A, on met en évidence certaines propriétés d’une fonction f qui seront utilisées
dans la partie B.

Partie A :

Soit f la fonction de la variable réelle x définie sur  par : .

1)      Déterminer les limites de f en  et .

2)      Calculer . En déduire le tableau de variation de f. Calculer .

3)      a) Etablir que l’équation  a deux solutions, une notée  appartenant à l’intervalle  et une autre notée  appartenant à l’intervalle .
b) Montrer que .
On démontrerait de même que  vérifie l’égalité : .

4)      Préciser le signe de  suivant les valeurs de x.

Partie B :

1)      Soit u la fonction de la variable réelle x définie sur  par : .
Etudier le sens de variation de u. On appellera  l’unique nombre réel solution de .

On admettra pour la suite que pour tout réel x, .

2)      Soit g_k la fonction définie sur  par .
On note C_k la courbe représentative de la fonction g_k dans le plan rapporté à un repère orthogonal.
a) Déterminer les limites de g_k en   et .
b) Prouver que .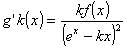
c) En déduire le tableau de variation de g_k. Calculer .

3)      On nomme M_k et N_k les points de la courbe C_k d’abscisses respectives  et .
a) En utilisant la question 3)b) (partie A), montrer que : .
b) Donner de même .
c) Déduire des questions précédentes que lorsque k varie, les points M_k et N_k sont sur une courbe fixe H dont on donnera une équation.

4)      Représentations graphiques pour des valeurs particulières de k :
a) Déterminer la position relative des courbes C₁ et C₂.
b) Prouver que .
c) En prenant comme unité 2 cm sur l’axe des abscisses et 4 cm sur l’axe des ordonnées, construire les courbes C₁, C₂ et H sur le même graphique.
On prendra ,  et .