Conformément aux conventions internationales
relatives à la propriété intellectuelle, cette oeuvre est protégée.
BACCALAURÉAT
GÉNÉRAL BLANC
Cliquez ici pour obtenir
le document au format Word97 compressé avec
winzip.
SESSION 2004
Série : S
L’utilisation d’une calculatrice autorisée.
Ce sujet comporte 4 pages numérotées de 1 à 4.
Le candidat doit traiter les DEUX exercices et le problème.
La qualité de la rédaction, la clarté
et la précision des raisonnements entreront pour
une part importante dans l’appréciation des copies.
page 1/4
Tournez la page S.V.P.
EXERCICE 1 (commun à tous les candidats) : 4 points
On dispose de deux urnes a et b contenant des boules blanches et des boules rouges indiscernables au toucher. L’épreuve consiste à choisir une urne parmi les urnes a et b proposées (le choix de l’urne est effectué au hasard, les deux choix sont équiprobables), puis à effectuer le tirage d’une boule dans l’urne choisie.
On note A l’événement « l’urne a est choisie », B l’événement « l’urne b est choisie » et R l’événement « une boule rouge est obtenue au tirage ».
On note pA(R) la probabilité conditionnelle de l’événement R par rapport à l’événement A.
1. Dans cette question, l’urne a contient une boule rouge et quatre boules blanches, l’urne b contient quatre boules rouges et deux boules blanches.
a) Déterminer les
probabilités suivantes : p(A), pA(R), p(A
R).
b) Montrer que p(R) =
.
c) Sachant que la boule obtenue est rouge, quelle est la probabilité que l’urne choisie soit l’urne a ?
2. Dans cette question, on suppose que l’urne a contient quatre boules blanches et l’urne b deux boules blanches. L’urne a contient en outre n boules rouges (où n désigne un entier naturel inférieur ou égal à 5), l’urne b en contient (5 - n).
a) Exprimer pA(R) et pB(R) en fonction de n .
b) Démontrer : p(R) =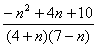 
.
c) On sait que n ne prend que six valeurs entières.
Déterminer la répartition des cinq boules rouges entre les urnes a et b donnant la plus grande valeur possible de p(R).
page 2/4
EXERCICE 2 (candidats n’ayant pas suivi l’enseignement de spécialité) : 5 points
Le plan est muni d’un repère orthonormal direct 
.
On prendra 2 cm pour unité graphique.
On considère l’application F du plan dans lui-même qui, à tout point M d’affixe z, associe le point M’ d’affixe z’ tel que :
1. Soit
A le point d’affixe 
.
Déterminer les affixes des points A’ et B vérifiant respectivement :
A’=F(A) et F(B) = A
2. Méthode de construction de l’image de M.
a) Montrer qu’il existe
un point confondu avec son image. On notera 
ce
point et 
son
affixe.
b) Etablir que, pour tout complexe z distinct de 
,
Soit M un point distinct de 
.
Comparer MM’ et M
et déterminer une mesure de l’angle (
,
). En déduire une méthode de construction de M’ à partir de M.
3. Etude de l’image d’un ensemble de points.
a) Donner la nature
et les éléments caractéristiques de l’ensemble (
)
des points du plan dont l’affixe z vérifie 
.
Vérifier que B est un point de (
).
b) Démontrer que pour tout z élément de 
,
.
Démontrer que l’image par F de tout point de (
)
appartient au cercle (
’)
de centre A’ et de rayon 2.
Placer 
,
A, B, A’, (
)
et (
’)
sur une même figure.
page 3/4
EXERCICE 2 (candidats ayant suivi l’enseignement de spécialité) : 5 points
1.
On considère l’équation (E) : 
où
x et y sont des entiers relatifs.
a) Déterminer un couple d’entiers relatifs 
tel
que 
;
en déduire une solution particulière 
de
l’équation (E).
b) Déterminer les couples d’entiers relatifs solutions de l’équation (E).
2.
Soit 
un
repère orthonormal de l’espace.
On considère le plan P d’équation : 
On considère les points du plan P qui appartiennent aussi
au plan 
.
Montrer qu’un seul de ces points a pour coordonnées des entiers naturels ; déterminer les coordonnées de ce point.
3. On considère un point M du plan P dont les coordonnées x, y et z sont des entiers naturels.
a) Montrer que l’entier y est impair.
b) On
pose 
où
p est un entier naturel.
Montrer que le reste dans la division euclidienne de 
par
3 est égal à 1.
c) On
pose 
où
q est un entier naturel.
Montrer que les entiers naturels x, p et q vérifient la
relation : 
.
En déduire que q prend les valeurs 0 ou 1.
d) En déduire les coordonnées de tous les points de P dont les coordonnées sont des entiers naturels.
page 3/4
PROBLEME (Commun à tous les candidats) : 11 points.
Partie A
L’objet de cette partie est l’étude de la fonction f définie
sur lR par 
.
On note (C) la courbe représentative de f dans un repère
orthonormé 
(unité
graphique : 3 cm).
1. On considère
la fonction g définie sur [0 ; +
[
par : 
.
a) Déterminer la dérivée g’ de la fonction g.
b) Donner le sens de variation de g, puis le signe de g.
2. Soit f’ la dérivée de f .
a) Montrer que, pour
tout réel x, 
.
b) En utilisant le 1. étudier le sens de variation de f.
3. a) Montrer
que, pour tout réel x, 
.
En déduire la limite de f(x) lorsque x tend vers +
.
b) Déterminer la limite de f(x) lorsque x tend vers -
.
4. Dresser le tableau de variation de f et tracer la courbe (C).
Partie B
L’objet de cette deuxième partie est l’étude d’une suite définie à partir de f.
Les calculs seront effectués à la calculatrice.
1. Démontrer
que l’équation f(x) = x admet une seule solution notée 
.
Montrer que 
.
2. Démontrer
que, pour tout réel x tel que 
on
a : 
et
.
3. On considère
la suite 
définie
par :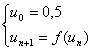 
a) En admettant que,
pour tout entier naturel n, 
,
démontrer par récurrence : 
En déduire que la suite 
converge
vers 
.
b) Déterminer le plus petit entier n0 tel que, pour tout entier n supérieur à n0 ,
.
Partie C
L’objet de cette partie est l’étude d’une primitive de f .
1. Montrer
que, pour tout réel x , 
2. En utilisant la question précédente calculer une primitive F de f.
Pour
contacter le webmaster 
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.