DEVOIR SURVEILLE N°1
Cliquez ici pour obtenir
le document au format Word compressé avec winzip.
Exercice n°1 : 3 points
Trouver, si elle existe, la limite de 
quand
x tend vers 1.
Exercice n°2 : 17 points
A) Soit g la fonction définie sur 
par :
.
On désigne par C sa courbe représentative dans un plan rapporté à un repère orthonormal 
.
1)
Trouver la limite de g
en 
.
Qu’en déduit on pour C ?
2)
Démontrer que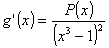 
avec
pour
tout x appartenant à I.
3)
Etudier les variations de P sur I et démontrer que
l’équation 
admet
une unique solution 
dans
I, vérifiant 
.
En déduire le signe de 
sur
I.
4) Déterminer les variations de g sur I.
5)
a) Déterminer une équation de
la tangente T à la courbe C au point 
.
b) Préciser la position de C par rapport à T.
B) Soit la fonction f définie par :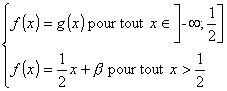
,
.
Trouver 
pour
que f soit continue en 
.