Secondes : Devoir Commun n°3, le Lundi 9 Février 2004
Ce devoir est d’une durée d’une heure, il sera tenu compte de la clarté
de la rédaction et de la précision des résultats dans l’appréciation de la copie.
|
de variations est donné ci-contre. De plus, on sait que : f(-2) = 0 f(4) = 0 et f(1) = 5 . 1) A
l’aide du tableau de variations et |
x -5 f 6 -3 -1 |
|
2) Que représente 6 pour la fonction f ? 3) Que
peut-on dire de f sur l’intervalle 4) Soit A(-2 ; 0) et B(1 ; 5). Donner l’expression de la fonction affine g dont la représentation graphique est la droite (AB). 5) Résoudre
graphiquement sur [-5 ; 8] l’inéquation |
|
Exercice 2 : Le repère 
est
orthonormal. Dans ce repère, A(-1 ; 6) B(5 ; 9) C(5 ;-6)
et D(1 ;2).
1) Démontrer que le triangle ABC est rectangle.
2)
Démontrer que les vecteurs 
et
sont
colinéaires, en précisant la valeur du coefficient de colinéarité k
tel que 
.
3) Quelles sont les coordonnées du point E tel que DBEC soit un parallélogramme ?
4) On appelle I le centre du cercle circonscrit au triangle ABC. Quelles sont les coordonnées de I ? Quel est le rayon de ce cercle ?
5) Montrer que le point F(11 ; -3) appartient au cercle circonscrit à ABC.
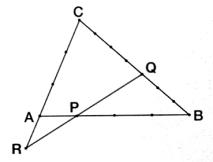Exercice 3 : ABC est un triangle ;
P un point de (AB), Q un point
de (BC) et R un point de (AC) disposés comme sur la figure
ci-contre (les graduations sur les droites sont régulières).
1)
Donner les valeurs des réels k, m et n tels que :
et 
.
2)
Montrer que 
.
3)
Exprimer 
en
fonction de 
et
.
4)
Justifier que 
.
Que peut-on en conclure ?
Pour
contacter le webmaster 
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.
8
?
.