Cliquez ici pour obtenir le document au format Word97 compressé avec winzip.
DEVOIR SURVEILLE N °
Exercice n°1 : 3 points
Le calife de Bagdad, espiègle, affirme : « J’ai un parc de 300 voitures, composé uniquement de Rolls et de Clio. Si je multiplie le nombre de Rolls par 2 et celui de Clio par 5, et si j’ajoute les deux résultats, j’obtiens 2000 ».
Expliquer pourquoi ce n’est pas possible.
Exercice n°2 : 5 points
On considère les points A(-3 ; 7), B(-7 ; -2) et C(4 ; 3).
1)
Calculer les coordonnées de G
tel que ![]() .
.
2)
Soit I le milieu de [BC]
et H le point de coordonnées ![]() .
.
Démontrer que les points A, I et H sont alignés.
3)
Trouver une relation entre ![]() .
.
Exercice n°3 : 8 points
ABCD est un rectangle de côtés AB = 7 cm et AD = 5 cm.
Sur chaque côté, on a placé les points M, N, P et Q tel que AM = BN = CP = DQ = x.
1) Donner un encadrement de x.
2) Démontrer que MNPQ est un parallélogramme.
3)
Calculer, en fonction de x,
l’aire S(x) de MNPQ.
Vérifier que ![]() .
.
4)
Calculer ![]() .
.
Montrer que ![]() .
.
En déduire le minimum de S sur [0 ; 5]. En quelle valeur est-il
atteint ?
5) Donner une représentation graphique de cette fonction, après avoir dressé un tableau de valeurs, pour x décrivant [0 ; 5] par pas de 0,5.
6) Dresser un tableau des variations de la fonction S.
7)
Comment choisir x pour que ![]() (à
justifier par un calcul).
(à
justifier par un calcul).
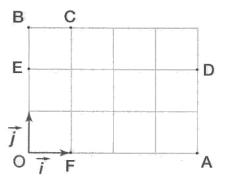
Exercice n°4 : 4 points
Sur la figure ci-contre, les points A, B, C, D, E et F ont des coordonnées entières.
1) Trouver, par le calcul, une équation des droites (AB), (CD) et (EF).
2) Démontrer que ces droites sont concourantes.
Pour
contacter le webmaster ![]() .
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.