Cliquez ici pour obtenir le document au format Word compressé avec winzip.

DEVOIR SURVEILLE N°

Exercice n°1 : 5,5 points

Soit une suite u définie par :

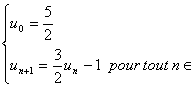
1)      Calculer u₁, u₂, u₃.

2)      Démontrer que si u_n est inférieur à 2, alors  aussi.

3)      On admet que . Etudier la monotonie de u.

4)      Soit la suite v telle que pout tout  on ait : .
a) Calculer v₀, v₁, v₂, v₃.
b) Exprimer  en fonction de v_n.

5)      Etudier la monotonie de la suite w définie par  pour tout .

Exercice n°2 : 6 points

Soit ABCD un tétraèdre et I le milieu de [AC].

E est un point de la droite (AB) et F un point de la droite (CD). On note G le milieu du segment [EF].

Le but de ce problème est de déterminer le lieu géométrique du point G lorsque les points E et F décrivent respectivement les droites (AB) et (CD).

1)      Expliquer pourquoi  est un repère de l’espace. Donner dans ce repère les coordonnées des points A, C, D et I.

2)      Justifier l’existence d’un réel t tel que .

3)      Démontrer que F a pour coordonnées (1-t ; t ; 0) dans .

4)      Justifier qu’il existe un réel m tel que E ait pour coordonnés (0 ;0 ;m) dans .

5)      Déterminer les coordonnées du point G en fonction des réels m et t.

6)      En déduire que : .

7)      Conclure.

Exercice n°3 : 8,5 points

Soit la fonction f définie sur  par :  où m et p sont des nombres réels quelconques.

1)      Justifier que f est définie sur .

2)      Calculer les nombres m et p pour que C, la courbe représentative de f, passe par le point A de coordonnées (2 ;0) et admette au point B, d’abscisse 1, une tangente parallèle à la droite d’équation.

3)      On considère la fonction g définie sur  par : .
a) Etudier les variations de g et ses limites en  et .
b) Montrer que la courbe C représentative de g admet une asymptote et donner son équation.
c) Prouver que C admet un centre de symétrie.
d) Construire C dans un repère orthonormal.
e) Soit  un nombre réel, démontrer que  est équivalent à .
f) En déduire graphiquement, selon les valeurs de , le nombre de solutions de l’équation .
g) En déduire, sans calculer le discriminant, le nombre de racines du polynôme :.