Cliquez ici pour obtenir le document au format Word compressé avec winzip.
DEVOIR SURVEILLE N°1
Exercice n°1 :
On considère la fonction f telle que :
.
1) Déterminer son ensemble de définition.
2)
Démontrer que f est la composée de deux fonctions usuelles.
3) En déduire le sens de variation de f sur I.
Exercice n°2 :
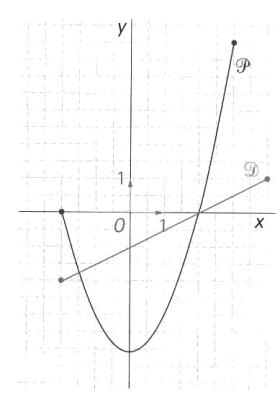
On a représenté ci-contre les courbes :
D d’équation 
et
P d’équation 
.
1) Quels sont les ensembles de définition de u ? de v ?
2)
Quels est l’ensemble des valeurs
de 
?
3)
a) Pourquoi peut-on définir la
fonction 
?
b) Trouver 
.
c) Etudier les variations de f sur [-2 ; 0] et sur [0 ; 4].
Exercice n°3 :
Soit les fonctions f et g définies sur 
par :
et
.
1) Etudier les variations de f et g.
2) En déduire les variations de la fonction f + g et de la fonction –2g.
3)
Déterminer 
et
sous
forme d’un quotient où le numérateur et dénominateur seront factorisés au maximum.
4)
Exprimer 
en
simplifiant au maximum l’écriture.
Pour
contacter le webmaster 
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.