Cliquez ici pour obtenir le document au format Word97 compressé avec winzip.
DEVOIR SURVEILLE N°
Exercice n°1 :
1)
a) Représenter sur le cercle trigonométrique, l’ensemble des points
M de coordonnées 
tel
que 
.(E)
b) En déduire l’ensemble des solutions de l’inéquation (E) sur 
,
puis sur 
.
2)
Simplifier l’expression 
.
Exercice n°2 :
1)
Soient les fonctions f et g définies par :
et
.
Déterminer l’expression des fonctions 
et
ainsi
que leur domaine de définition.
2)
Trouver, en justifiant les étapes,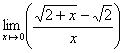 
.
En déduire 
pour
h étant la fonction racine carrée.
Exercice n°3 :
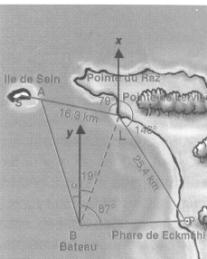
Le commandant du bateau situé en B fait le point.
Il relève les mesures d’angles PBy = 87° et LBy = 19°.
Il souhaite déterminer le cap pour passer au point A, entre l’île de Sein et la points du Raz.
Sur la carte, il relève les distances en kilomètres : AL = 16,3 ; LP = 25,4 et les mesures d’angles PLx = 146° et ALx = 79°.
Ls demi-droites [By) et [Lx) sont dirigées vers le nord.
1) Démontrer que BLP = 53°.
2) Calculer BL.
3) Calculer la mesure en degrés de l’angle ABy.
Exercice n°4 :
ABCDE est un pentagone régulier direct inscrit dans le cercle trigonométrique C de centre O.
1)
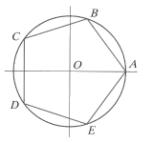a) Indiquer les mesures des angles orientés : 
.
b) Exprimer 
et
en
fonction du vecteur 
.
2)
a) On appelle 
l’isobarycentre
des points A,B, C, D et E.
Démontrer que O est barycentre des points pondérés : 
et
.
Que peut-on en déduire pour O,A et 
?
b) On considère la rotation de centre O et d’angle 
.
Comment transforme-t-elle le pentagone ABCDE ?
En déduire que 
,
O et B sont alignés.
c) Que peut-on conclure pour le point 
et
pour 
?
3)
a) Résoudre l’équation 
dans
.
b) Démontrer que 
est
solution de cette équation.
c) En déduire la valeur exacte de 
,
ainsi que celle de 
.
Exercice n°5 :
PARTIE A :
On considère la fonction f définie sur 
par
.
On désigne par C sa courbe représentative dans un repère orthogonal
.
On prendra 4 cm pour une unité sur l’axe des abscisses et 1 cm pour une unité sur l’axe des ordonnées.
1)
Déterminer les limites de f
en 
.Quelle
conséquence graphique en tire-t-on pour C ?
2)
a) Déterminer les limites de f en 
et
en 
.
b) Déterminer les réels a, b et c tels que, pour tout x
différent de 
,
.
En déduire que la droite D
d’équation 
est
asymptote oblique à C en 
et
.
Etudier la position relative de D et C.
3)
a) Calculer la dérivée 
de
f.
b) Etudier les variations de f et dresser son tableau de variations.
4) On appelle I le point d’intersection des deux asymptotes de C. Démontrer que I est le centre de symétrie de C.
5) Construire C et ses asymptotes en précisant aussi les points à tangente horizontale.
6)
Déterminer graphiquement le nombre de solutions de l’équation
où
k est un nombre réel donné. (On discutera suivant les valeurs de k.)
PARTIE B :
On considère la fonction g, définie sur le même
ensemble que f par 
.
Dans le repère 
,
on désigne par 
sa
courbe représentative, par M, N et P les points d’abscisse
x, placés respectivement sur C,
et
D (avec 
).
1)
Calculer 
.
Comment ce résultat se traduit pour les points M, N et P ?
En déduire que C
et 
ont
les mêmes asymptotes.
2)
Calculer 
où
est
la dérivée de g, et en déduire les variations de g.
3)
Tracer 
sur
le même graphique que C.
Pour
contacter le webmaster 
.
Pour signer le
livre d'or .
Problème
de résolution des exercices ? allez sur le Forum.