Accès direct à : classe 6ème 5ème 4ème 3ème 2nde 1ère S 1ère ES Tle S Tle ES

section du site Accueil Le mexique Games

DEVOIR SURVEILLE N°1
Cliquez ici pour obtenir le document au format Word97 compressé avec winzip.

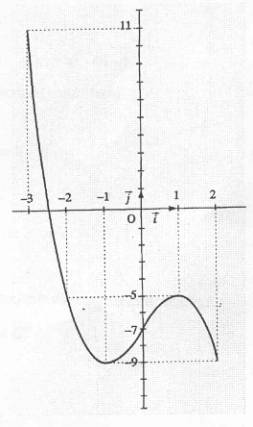
Exercice n°1 :

Dans le graphique ci-dessous la courbe (C) représente, dans un repère orthogonal (O ;, ) une fonction f définie sur l'intervalle [-3 ; 2].

1)      a) Par lecture graphique, déterminer les valeurs de f(1) et de f(-l).
b) On suppose que f possède sur l'intervalle [-3 ; 2] une fonction dérivée que l'on désigne par f'. Déterminer la valeur de f'(1)et le signe de f'(0).

2)      Dresser le tableau de variation de la fonction f.

3)      On admet que, pour tout x de l'intervalle [-3 ; 2], on a
f(x) = ax³ + cx + d où a, c et d sont des nombres réels.
a) Déterminer l'expression de f'(x) en fonction de a, c et x.
b) En utilisant les résultats du l), déterminer les valeurs de a, c et d.

4)       Par simple lecture graphique, déterminer:
a) Le nombre de solutions, dans l'intervalle [-3 ; 2], de l'équation f(x) = -7.
b) Les valeurs des solutions, dans l'intervalle [-3 ; 2], de l'équation f(x)= -5.

Exercice n°2 :

Soit f la fonction définie sur l'intervalle par :  et C sa courbe représentative.

1)      Etudier le sens de variation de f sur  et dresser son tableau de variation.

2)      Déduire de l'étude précédente que l'équation f(x) = 0 admet deux solutions dans l'intervalle .

3)      Déterminer une valeur approchée à 10^-2 près de chacune de ces solutions.

4)      Trouver l'équation de la tangente T à la courbe C  au point d'abscisse 2.

5)      Construire la courbe C et la droite T sur l'intervalle  en utilisant une échelle adaptée.

Exercice n°3 :

1)      Soit g la fonction définie sur  par . Calculer g' puis g''.
Quelle relation simple peut-on trouver entre g et g'' ?

2)      Déterminer les fonctions dérivées des fonctions  suivantes :
 définie sur ;
 définie sur ;
et  définie sur ]4;+¥[.